Learning to Control Buildings Like an Engineer
A new approach to energy-efficient HVAC control infuses deep learning with guidance from physics.

Buildings are a big deal for climate change. They contribute to 40% of global energy use, with a large portion of that energy going to heating, cooling, ventilation, and air-conditioning (HVAC).
AI can play a major role in reducing that energy use. Switching to AI-based control can reduce energy use and greenhouse gas emissions by 13-28%. In fact, if all buildings were operated by advanced AI systems, we could reduce the global energy/emission bill by at least 4%!
Nonetheless, in most 21st-century buildings, HVAC systems are still controlled by “dumb” rule-based controllers (RBC) that are designed and tuned by hand. Why are we not already using advanced AI to improve the energy efficiency of buildings at scale?
The problem is that switching to AI control isn’t as easy as replacing your smartphone or buying a new car. Buildings are made to last, and even worse, each building has a unique layout, infrastructure, location, and set of user profiles. All of this makes modernization very costly.
In this post, I focus on the problem of designing advanced control methods for HVAC systems in a cost-efficient way. In particular, I discuss how to augment data-driven deep learning with domain-aware physics-based control using a hybrid method called differentiable predictive control (DPC). DPC essentially allows a data-driven system to incorporate an approximate physics simulator into its training. This enables it to learn a reliable, interpretable model with far less training data than previous data-driven methods.
Which way to the promised land?
Currently, engineers design smart HVAC control systems using two competing approaches, model-based and data-driven methods.
In model-based approaches, the advanced controller is designed by engineers from known physical laws. If done diligently, model-based methods, the most popular of which is called model predictive control (MPC), can provide outstanding performance with safety guarantees.
In an ideal world, then, engineers would simply deploy an MPC system for each new building. Unfortunately, each new building’s model must be designed by a human expert, making this method tedious and costly in practice. These controllers are also expensive to maintain due to complex optimization routines that need to run in real-time.
The main alternative is data-driven approaches such as deep reinforcement learning (RL), which promise automated controller design via the powers of machine learning. Unfortunately, purely data-driven approaches do not provide safety and performance guarantees. They also must learn the best control policies without any knowledge of how buildings and temperatures work, which often requires prohibitively large datasets.
We can deal with this conundrum by fusion. Not nuclear fusion (though it would be cool to have a portable tokamak in the garage!), but rather by fusing model-based and data-driven AI methods for optimal control design.
In a recent series of papers, my PNNL colleagues and I described a new method called differentiable predictive control (DPC) for learning model-based HVAC control policies. The core idea is to create a neural network that approximates a building’s thermal dynamics. This model can then be incorporated directly into a deep reinforcement learning controller to help train the overall system.
Our method has two steps, illustrated in the figure below. We start from a real-world dataset of climate conditions, HVAC settings, measured building temperatures, and so forth for a given building. With that data, we first train a data-driven predictive model of the building dynamics, designed to prefer models that exhibit known physics-based behaviors. Second, we use the learned model, known performance metrics, and physics-derived constraints and optimization penalties to optimize the control policy in a domain-aware way.
As a result, we obtain a highly effective method that combines the benefits of both worlds. Thanks to machine learning, it can quickly adapt to new scenarios. And thanks to inductive biases drawn from physics, it can do so using small datasets while satisfying operational constraints.
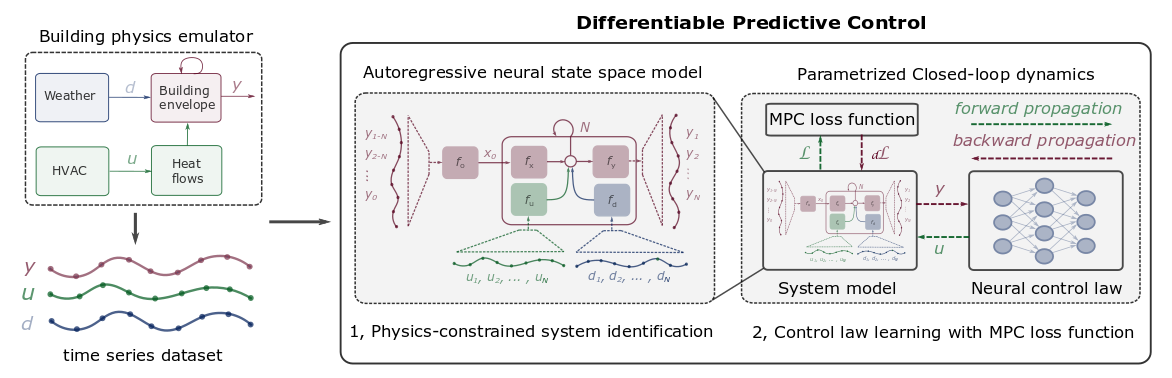
Step 1: Physics-Constrained Neural Surrogate Model of the Building Dynamics
In the first step, we automatically learn the thermal behavior of a given building via a physics-constrained neural state-space model (SSM). The model has a set of state variables, representing the temperatures of the building walls and indoor environment, and a set of control inputs, which are manipulable variables of the HVAC system such as mass flow rates and supply temperatures. We also consider a set of measurable disturbances representing the environmental factors such as ambient temperature and solar irradiation. Then, given a time-series dataset, we train this SSM model to predict the future evolution of the indoor temperatures that satisfy a set of high-level constraints inspired by laws of thermodynamics.
We structure the computational graphs of these models to mimic the dynamics of physical buildings. We decompose the whole system into subsystems, or blocks, where each of the blocks represents a different part of the physical system—e.g., the building envelope, HVAC system, or influence of weather conditions. To make the model easily transferable to different types of buildings and operational conditions, we represent each individual block by a deep neural networks.
To improve accuracy and generalization, we guide the neural networks by penalizing violations of certain thermodynamic laws. One key physics insight is that a building represents a dissipative system evolving to achieve thermal equilibrium with the environment. This inspired us to enforce constraints on the model that can be interpreted as promoting the dissipativeness of an abstract dynamical system. Furthermore, using an optimization strategy known as the penalty method, we can further nudge our model to keep its states within physically realistic bounds.
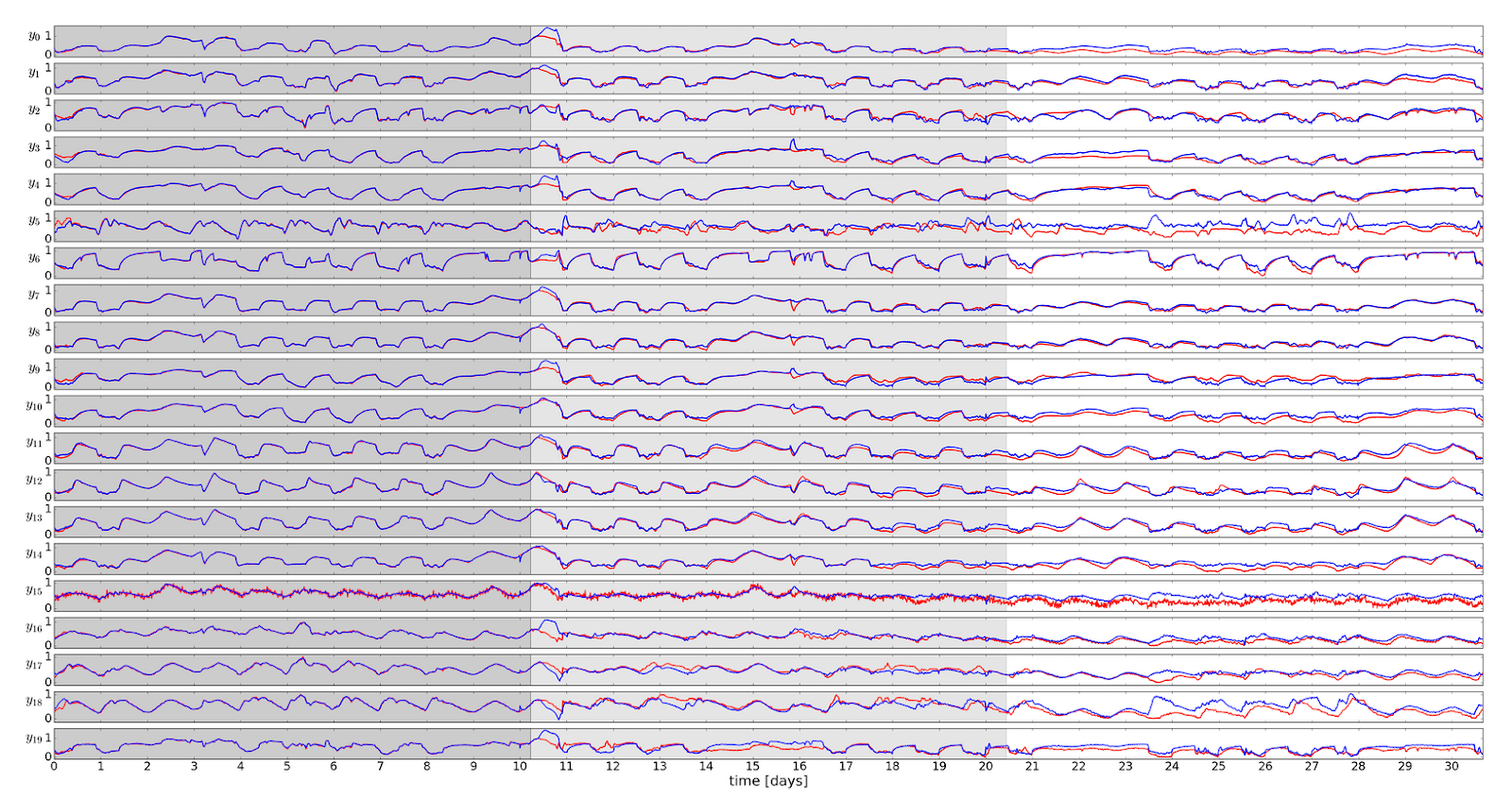
In a case study, we demonstrate the learning of a thermal dynamics model for a real-world building, given a limited amount of measurement data. For our experiments, we did not have access to the full real-world dataset, so we instead used a simulated dataset generated by a pre-existing physics emulator, which models a building’s thermal dynamics reasonably accurately.) We considered a commercial office building with a typical setup, including air handling units, 20 thermal zones, a natural gas boiler, hot water reheat coils, and a central chiller plant. When we trained and validated our system on just 20 days of data (with less than 100 data points per day), it predicted the next 10 days’ thermal behavior with less than 50% of the error rate of previous data-driven methods.
Step 2: Differentiable Predictive Control
Once we have an accurate model of the building’s thermal dynamics, we can proceed to the second step, model-based policy optimization.
In conventional RL approaches, the system must learn everything from scratch. It has no model of the building and or of thermodynamics; all it has is measurement data and some “reward signal” indicating how well a given set of control decisions performed. Even if the reward signal comes from a physics model, rather than the actual building, learning a control policy in this way is still extremely inefficient.
We could mitigate this problem if we could prime the RL system with a model of the building’s thermal dynamics. That way, the only thing to learn by reinforcement would be the control policy; the building model would already know how the environment behaves. But to leverage an embedded building simulation, each round of training would have to try a control policy, run the building simulation, calculate the reward/error for the results, and adjust the neural network parameters for the control policy accordingly. With a conventional physics-based simulator, there is no way to propagate the reward/error signal back to determine how to adjust the control parameters.
This is where our neural surrogate model comes in. Because our approximate model of the building’s physics is itself a neural network, it is fully differentiable, meaning we can leverage the powerful automatic differentiation tools underlying all practical successes of deep learning. This design trick allows us to backpropagate the control performance metrics (rewards and constraint violation penalties) through the system dynamics model to optimize the policy parameters directly. Thus, the reinforcement learning only has to tune the control parameters; it does not need to learn the environment dynamics. As a result, the DPC method is much more sample-efficient (and interpretable!).
Now we are well equipped to deal with the challenging problem of controlling the heating system of a multi-zone building. We train the DPC policies by sampling expected operational conditions from the learned surrogate model and letting training work out optimal policies for those scenarios. The control performance of the trained DPC policy is shown below.

Finally, we validate the DPC method’s performance in a case study using a physics-based simulator of the thermal dynamics in a multi-zone building. Our results indicate that DPC can handle economic objectives subject to dynamic constraints imposed on nonlinear system dynamics with multiple inputs and outputs.
Conclusion
Energy-efficient building controls could be revolutionized by reliable, data-driven methods that are cost-effective in terms of computational demands, data collection, and domain expertise. Our two-step DPC learning method is a large step toward this goal.
The DPC approach does not require the large time investments by domain experts and extensive computational resources demanded by physics-based emulator models. Based on only ten days’ measurements, we significantly improved on prior state-of-the-art results for a modeling task using a large-scale office building dataset.
Additionally, in a simulation case study using a multi-zone building thermal dynamics model, we showed that it is possible to learn control policies for constrained optimal control problems with a large number of states over long prediction horizons.
Based on the presented features, we believe that the proposed DPC method has long-term potential for research and practical applications. DPC is particularly appealing for scenarios that require fast development and low-cost deployment and maintenance on hardware with limited computational resources. More fundamental and practical work needs to be done to further verify the real-world performance, but we are optimistic about the promise of these fusion-based methods.
